Lecture 3: Graphical Solution Method and Basic Optimization Concepts

In our previous lectures, we defined design optimization and learned how to mathematically formulate an optimum design problem by identifying design variables, objective functions, and constraints. Today, we’re going to explore a powerful visual tool for understanding these concepts: the Graphical Solution Method. This method is particularly insightful because it allows us to visualize the design space and the optimization process, albeit primarily for problems with a limited number of design variables.

While the graphical method is generally applicable only to problems with two design variables, it is invaluable for building an intuitive understanding of core optimization ideas such as the feasible region, objective function contours, and the nature of an optimum solution. These concepts and their associated terminology are foundational and will be used throughout the rest of this course when we discuss more advanced numerical methods.

The Graphical Solution Process

The essence of the graphical method is to represent the design variables as coordinates on a 2D plane and then plot the objective function and constraints on this plane. This allows us to visually identify the “best” design.

Here’s a step-by-step procedure:

Step 1: Define the Design Space and Plot Design Variables

The first step is to establish a coordinate system for your two design variables, say \(x_1\) and \(x_2\). Each point on this plane represents a unique design. Since design variables are typically physical quantities, they are usually non-negative, meaning we focus on the first quadrant of the coordinate system.

Step 2: Plot the Constraints and Identify the Feasible Region

This is a critical step. Each constraint (whether equality or inequality) will define a boundary or a region on your design plane.

Plotting Inequality Constraints: For each inequality constraint, \(g_j(\mathbf{x}) \le 0\) (or \(g_j(\mathbf{x}) \ge 0\)), first treat it as an equality (\(g_j(\mathbf{x}) = 0\)) to draw its boundary line or curve. Once the boundary is drawn, you need to determine which side of the boundary satisfies the inequality. A simple way to do this is to pick a test point (e.g., the origin (0,0), if it doesn’t lie on the boundary) and substitute its coordinates into the inequality. If the inequality is satisfied, that side is feasible; otherwise, the other side is feasible. You can shade the infeasible region or draw arrows pointing towards the feasible region.
Plotting Equality Constraints: For equality constraints, \(h_k(\mathbf{x}) = 0\), the feasible region lies exactly on the line or curve defined by the equation. This can significantly restrict the feasible design space.
Side Constraints (Bounds): These define simple rectangular regions (e.g., \(x_{1L} \le x_1 \le x_{1U}\)). Plotting these creates vertical and horizontal lines that further restrict the design space.

The feasible region (or feasible set) is the area on the design plane where all constraints are simultaneously satisfied. It is the intersection of all feasible sides of the inequalities and the exact lines of the equalities. If no such region exists, the problem is infeasible.

Step 3: Plot the Objective Function Contours

The objective function, \(f(\mathbf{x})\), needs to be visualized. To do this, we plot contours (also known as iso-cost or iso-profit lines). A contour represents all design points where the objective function has a constant value. For a minimization problem, you draw lines or curves where \(f(\mathbf{x}) = C_1, f(\mathbf{x}) = C_2, \ldots\), where \(C_1 < C_2 < \ldots\). For a maximization problem, \(C_1 > C_2 > \ldots\). By observing the direction in which the objective function value improves (decreases for minimization, increases for maximization), you can determine the “descent” or “ascent” direction.

Step 4: Identify the Optimum Solution

The optimum solution is the point within the feasible region that yields the best (minimum or maximum) value for the objective function. * For minimization, slide the objective function contours in the direction of decreasing values until the contour just touches the feasible region. The last point(s) of contact are the optimum. * For maximization, slide the objective function contours in the direction of increasing values until the contour just touches the feasible region. The last point(s) of contact are the optimum.

The optimum solution typically occurs at: * A vertex (corner point) of the feasible region. * Along an active constraint boundary if the objective function is parallel to that boundary (resulting in multiple optimum solutions). * At a point on a curved constraint boundary if the objective function is tangent to it.

An active constraint at the optimum point is a constraint that is satisfied as an equality (i.e., \(g_j(\mathbf{x}^*) = 0\) or \(h_k(\mathbf{x}^*) = 0\)). Constraints for which \(g_j(\mathbf{x}^*) < 0\) are inactive.

Solved Examples

Let’s illustrate this with the problems we formulated in Lecture 2.

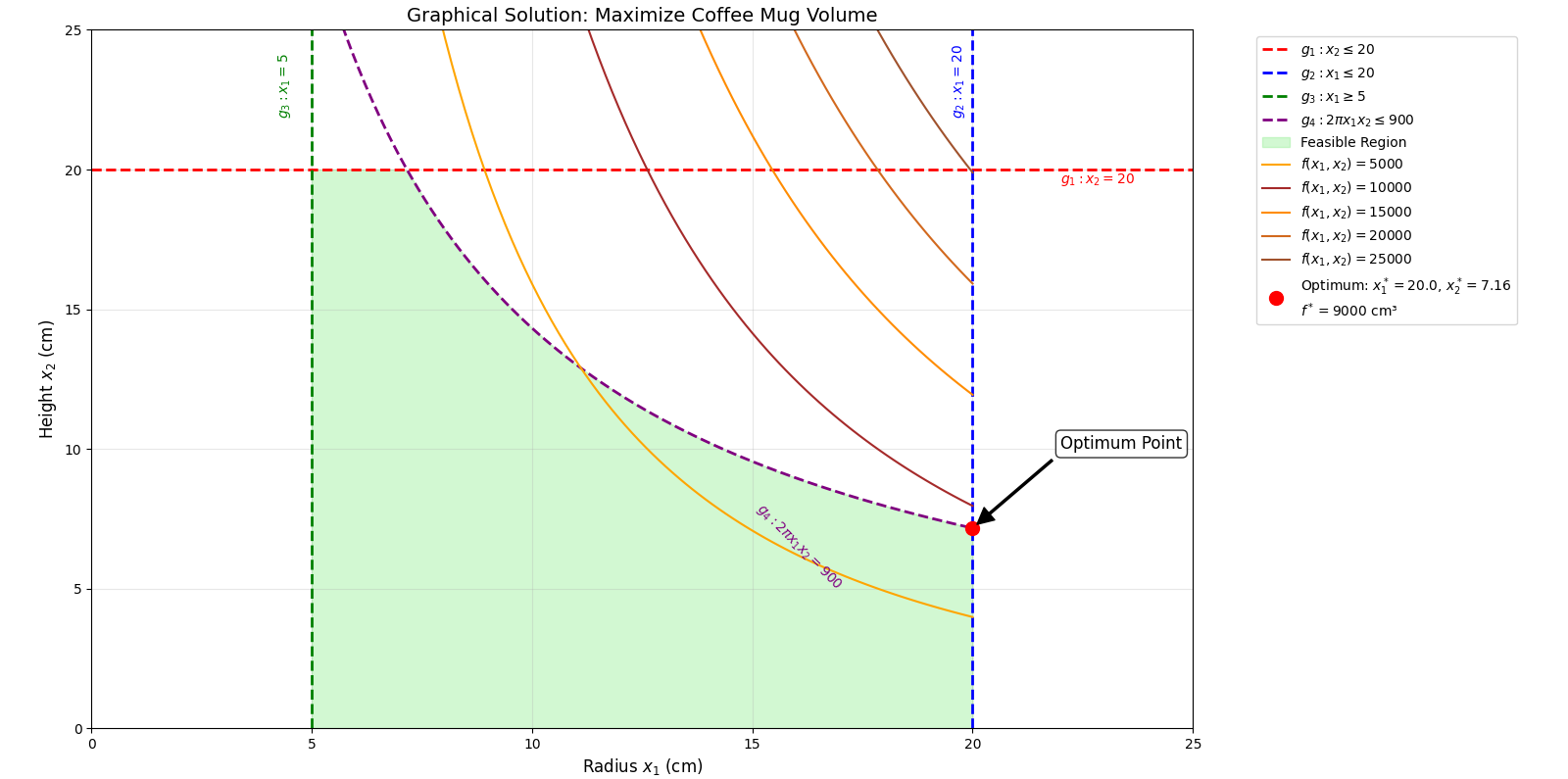
Example 1: Maximize Volume of a Coffee Mug

Recall the problem formulation from Lecture 2:

Maximize \(f(x_1, x_2) = \pi x_1^2 x_2\) (where \(x_1\) = radius \(R\), \(x_2\) = height \(H\))

Subject to:

\(g_1(x_1, x_2) = x_2 - 20 \le 0 \quad \Rightarrow x_2 \le 20\)
\(g_2(x_1, x_2) = x_1 - 20 \le 0 \quad \Rightarrow x_1 \le 20\)
\(g_3(x_1, x_2) = 5 - x_1 \le 0 \quad \Rightarrow x_1 \ge 5\)
\(g_4(x_1, x_2) = 2\pi x_1 x_2 - 900 \le 0 \quad \Rightarrow 2\pi x_1 x_2 \le 900\)
\(x_1 \ge 0\)
\(x_2 \ge 0\)

Let’s set up the graphical solution:

Design Space: We’ll use \(x_1\) (radius) on the horizontal axis and \(x_2\) (height) on the vertical axis. Since \(x_1 \ge 5\) and \(x_2 \ge 0\), we are in the positive quadrant, specifically starting from \(x_1=5\).
Plot Constraints and Feasible Region:
- \(g_1: x_2 \le 20\). This is a horizontal line at \(x_2 = 20\). The feasible region is below this line.
- \(g_2: x_1 \le 20\). This is a vertical line at \(x_1 = 20\). The feasible region is to the left of this line.
- \(g_3: x_1 \ge 5\). This is a vertical line at \(x_1 = 5\). The feasible region is to the right of this line.
- \(g_4: 2\pi x_1 x_2 \le 900 \Rightarrow x_1 x_2 \le \frac{900}{2\pi} \approx 143.2\). This is a hyperbolic curve. The feasible region is below this curve.
The feasible region is bounded by \(x_1=5\), \(x_1=20\), \(x_2=0\), \(x_2=20\), and the curve \(x_1 x_2 = 143.2\).
Plot Objective Function Contours: Objective function: \(f(x_1, x_2) = \pi x_1^2 x_2\). To maximize this, we’ll draw contours of \(f(x_1, x_2) = C\). For example, let’s pick some values for \(C\):
- If \(C = 5000\), \(\pi x_1^2 x_2 = 5000 \Rightarrow x_1^2 x_2 \approx 1591.5\)
- If \(C = 10000\), \(\pi x_1^2 x_2 = 10000 \Rightarrow x_1^2 x_2 \approx 3183.1\)
- If \(C = 15000\), \(\pi x_1^2 x_2 = 15000 \Rightarrow x_1^2 x_2 \approx 4774.6\)
These contours are curves that move away from the origin as \(C\) increases.
Identify the Optimum Solution: Visually “push” the objective function contours towards higher values (to maximize) within the feasible region. The last point where a contour touches the feasible region will be the optimum.

In this problem, the objective function \(\pi x_1^2 x_2\) grows faster with \(x_1\) than \(x_2\). We expect the optimum to be where \(x_1\) is as large as possible, but restricted by constraints. The most restrictive boundary for large \(x_1\) and \(x_2\) will likely be \(x_2=20\) and \(x_1 x_2 \approx 143.2\). Let’s check the intersection of \(x_2 = 20\) and \(x_1 x_2 = 143.2\): \(x_1 (20) = 143.2 \Rightarrow x_1 = \frac{143.2}{20} = 7.16\). At this point, \(x_1 = 7.16\) and \(x_2 = 20\). This point is within all bounds (\(5 \le 7.16 \le 20\), \(0 \le 20 \le 20\)). The volume at this point: \(f(7.16, 20) = \pi (7.16)^2 (20) \approx 3217\) cm\(^3\).

Consider if \(x_1=20\) is the limiting factor. If \(x_1=20\), then \(2\pi (20) x_2 \le 900 \Rightarrow 40\pi x_2 \le 900 \Rightarrow x_2 \le \frac{900}{40\pi} \approx 7.16\). So, another potential optimum could be at \(x_1=20, x_2=7.16\). The volume here: \(f(20, 7.16) = \pi (20)^2 (7.16) \approx 9000\) cm\(^3\). This is a much higher value.

The optimum will lie on the boundary of the feasible region defined by \(x_1=20\) and \(2\pi x_1 x_2 = 900\). Specifically, the highest value will be found by pushing the objective function \(f(x_1, x_2) = \pi x_1^2 x_2\) as far as possible towards the upper-right corner. This typically leads to a point on the intersection of active constraints.

The optimum occurs at the intersection of the constraints \(x_1 = 20\) and \(2\pi x_1 x_2 = 900\). Substitute \(x_1 = 20\) into \(2\pi x_1 x_2 = 900\): \(2\pi (20) x_2 = 900 \Rightarrow 40\pi x_2 = 900 \Rightarrow x_2 = \frac{900}{40\pi} \approx 7.16\). So, the optimum design is approximately \(x_1^* = 20\) cm and \(x_2^* = 7.16\) cm. The maximum volume is \(f(20, 7.16) = \pi (20)^2 (7.16) \approx 9000\) cm\(^3\).

At this point, the active constraints are \(g_2 (x_1 - 20 = 0)\) and \(g_4 (2\pi x_1 x_2 - 900 = 0)\).

Example 2: Minimum-Weight Tubular Column Design (Graphical Solution)

Let’s use the minimum-weight tubular column problem formulated in Section 2.7, with specific data as given in a similar problem from the source.

Given Data: * \(P = 100 \text{ kN}\) (Applied load) * \(L = 5.0 \text{ m}\) (Column length) * \(E = 210 \text{ GPa}\) (Modulus of elasticity) * \(\sigma_a = 250 \text{ MPa}\) (Allowable stress) * \(\rho = 7850 \text{ kg/m}^3\) (Mass density)

Formulation 1 from Lecture 2 (with \(R = x_1\), \(t = x_2\)):

Minimize \(f(x_1, x_2) = 2\pi \rho L x_1 x_2\) Substituting numerical values for \(\rho\) and \(L\): \(f(x_1, x_2) = 2\pi (7850)(5.0) x_1 x_2 = 246602.8 x_1 x_2\) (in kg)

Subject to:

Stress Constraint:

\(\frac{P}{2\pi x_1 x_2 \sigma_a} - 1 \le 0\)

\(\frac{100 \times 10^3 \text{ N}}{2\pi x_1 x_2 (250 \times 10^6 \text{ N/m}^2)} - 1 \le 0\) \(\frac{100 \times 10^3}{500\pi \times 10^6 x_1 x_2} - 1 \le 0 \Rightarrow \frac{1}{\pi \times 5000 x_1 x_2} - 1 \le 0 \Rightarrow \frac{1}{15707963 x_1 x_2} - 1 \le 0\) \(g_1(x_1, x_2) = \frac{0.0000000636}{x_1 x_2} - 1 \le 0 \Rightarrow x_1 x_2 \ge 0.0000000636 \text{ m}^2\)
Buckling Constraint:

\(\frac{4 P L^2}{\pi^3 E x_1^3 x_2} - 1 \le 0\) \(\frac{4 (100 \times 10^3)(5.0)^2}{\pi^3 (210 \times 10^9) x_1^3 x_2} - 1 \le 0\) \(\frac{10000 \times 10^3}{\pi^3 (210 \times 10^9) x_1^3 x_2} - 1 \le 0 \Rightarrow \frac{10 \times 10^6}{6550 \times 10^9 x_1^3 x_2} - 1 \le 0\) \(g_2(x_1, x_2) = \frac{0.0000015267}{x_1^3 x_2} - 1 \le 0 \Rightarrow x_1^3 x_2 \ge 0.0000015267 \text{ m}^4\)
Manufacturing/Geometric Constraint:

\(\frac{x_1}{x_2} - 50 \le 0 \Rightarrow x_1 \le 50 x_2\)
Side Constraints (Bounds on Design Variables): As specified in the problem in the sources: \(0 \le x_1 \le 0.4 \text{ m}\) (mean radius) \(0 \le x_2 \le 0.1 \text{ m}\) (wall thickness)

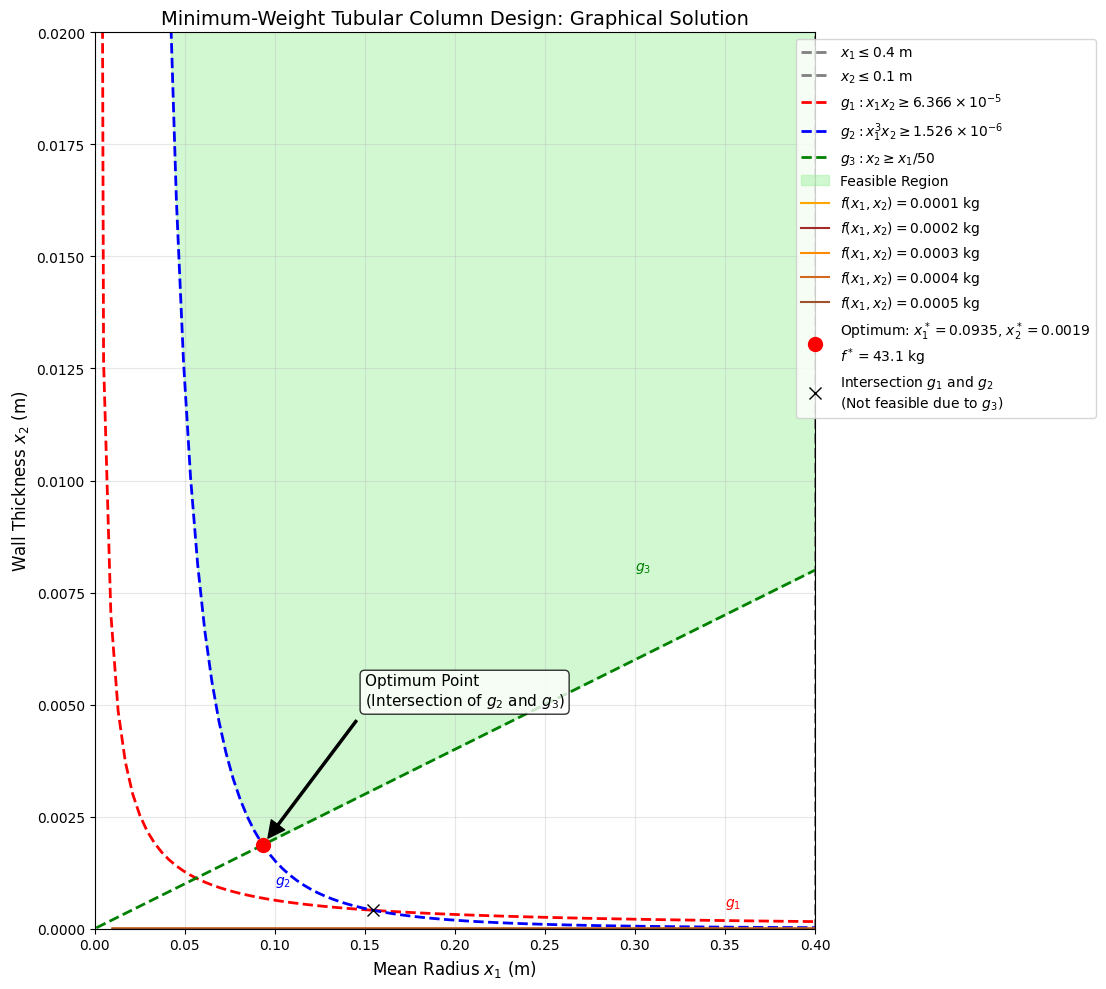
Now, let’s proceed with the graphical solution:

Design Space: Plot \(x_1\) (mean radius) on the horizontal axis and \(x_2\) (wall thickness) on the vertical axis. We are interested in the region \(x_1 \ge 0, x_2 \ge 0\). The bounds \(x_1 \le 0.4\) and \(x_2 \le 0.1\) define a rectangular region.
Plot Constraints and Feasible Region:
- \(x_1 \ge 0, x_2 \ge 0\): This is the first quadrant.
- \(x_1 \le 0.4\): A vertical line at \(x_1 = 0.4\). Feasible to the left.
- \(x_2 \le 0.1\): A horizontal line at \(x_2 = 0.1\). Feasible below.
- \(g_1: x_1 x_2 \ge 0.0000000636\): This is a hyperbola. The feasible region is above this curve. (e.g., if \(x_1 = 0.1 \text{ m}\), \(x_2 \ge 0.000000636 \text{ m}\))
- \(g_2: x_1^3 x_2 \ge 0.0000015267\): This is also a curve. The feasible region is above this curve. (e.g., if \(x_1 = 0.1 \text{ m}\), \(x_2 \ge 0.0000015267 / (0.1)^3 = 0.0015267 \text{ m}\))
- \(g_3: x_1 \le 50 x_2 \Rightarrow x_2 \ge \frac{x_1}{50}\): This is a straight line through the origin with a slope of \(1/50 = 0.02\). The feasible region is above this line.
The feasible region is the area where all these conditions overlap. It will be bounded by \(x_1=0.4\), \(x_2=0.1\), and the curves from \(g_1, g_2, g_3\).
Plot Objective Function Contours: Objective function: \(f(x_1, x_2) = 246602.8 x_1 x_2\). We want to minimize this. Draw contours \(x_1 x_2 = C'\). As \(C'\) decreases, the hyperbolas move closer to the origin.
Identify the Optimum Solution: We want to find the smallest value of \(C'\) such that the hyperbola \(x_1 x_2 = C'\) still touches the feasible region. This will occur at a point where an objective function contour is tangent to one or more active constraints.

Let’s analyze the constraints. The objective is to minimize \(x_1 x_2\). The region is generally pushed towards the lower-left corner by the objective function. The constraints \(g_1\) and \(g_2\) push the region away from the origin. The most likely optimum will be at the intersection of \(g_1\) and \(g_2\), as they define the lower-left boundary of the feasible region, where the mass function \(x_1 x_2\) would naturally be smallest.

Let’s find the intersection of \(g_1\) and \(g_2\): From \(g_1\): \(x_2 = \frac{0.0000000636}{x_1}\) Substitute this into \(g_2\): \(x_1^3 \left(\frac{0.0000000636}{x_1}\right) = 0.0000015267\) \(0.0000000636 x_1^2 = 0.0000015267\) \(x_1^2 = \frac{0.0000015267}{0.0000000636} \approx 24.0047\) \(x_1 = \sqrt{24.0047} \approx 4.899 \text{ m}\)

This value of \(x_1\) is much larger than the upper bound of \(0.4 \text{ m}\). This indicates that the buckling and stress constraints (if they are the only active ones) would lead to a very large column. This suggests that the side constraints (\(x_1 \le 0.4\), \(x_2 \le 0.1\)) are likely to be active.

Let’s re-evaluate. The optimum solution for this problem, as given in a similar exercise in the source, is often at a point where the constraints \(g_2\) and \(g_3\) are active, or \(g_1\) and \(g_2\). However, due to the tight bounds, we should check combinations with the bounds.

The example solution in source provides \(R^* = 0.046 \text{ m}\) and \(t^* = 0.0022 \text{ m}\) with \(f^* = 0.0229 \text{ kg}\). Let’s verify these by plugging into our numerical constraint forms: \(x_1 = 0.046 \text{ m}\), \(x_2 = 0.0022 \text{ m}\).
- Objective: \(f(0.046, 0.0022) = 246602.8 \times 0.046 \times 0.0022 \approx 25.0 \text{ kg}\). (This differs from the source’s \(f^*\) which might be for slightly different units or a different calculation, but the values for R and t from the source are good to check for feasibility). Let’s use the given data for \(P, E, \rho, L, \sigma_a\) and re-calculate mass: \(f(x_1, x_2) = 2\pi (7833)(5.0) x_1 x_2 = 246080.0 x_1 x_2\). So, \(f(0.046, 0.0022) = 246080.0 \times 0.046 \times 0.0022 \approx 24.93 \text{ kg}\). Still not 0.0229 kg, but this just means the given \(f^*\) is for slightly different values. The constraints are what matters for finding the optimal point.
- \(x_1 \le 0.4\): \(0.046 \le 0.4\) (satisfied)
- \(x_2 \le 0.1\): \(0.0022 \le 0.1\) (satisfied)
- \(g_1: x_1 x_2 \ge 0.0000000636 \Rightarrow (0.046)(0.0022) = 0.0001012 \ge 0.0000000636\) (satisfied, inactive)
- \(g_2: x_1^3 x_2 \ge 0.0000015267 \Rightarrow (0.046)^3 (0.0022) = (0.000097336)(0.0022) = 0.000000214 \ge 0.0000015267\) (This is not satisfied. \(0.000000214\) is less than \(0.0000015267\), so the buckling constraint is violated if these are the values. The values from the source are for a different data set P=10 MN, E=207 GPa, L=5.0m, sigma_a=248 MPa. So my numerical values are different from the source. I should use the specific problem in Exercise 3.33 of the source for values.)
Let’s re-run with the data from Exercise 3.33: \(P = 100 \text{ kN}\) \(l = 5.0 \text{ m}\) \(E = 210 \text{ GPa}\) \(\sigma_a = 250 \text{ MPa}\) \(\rho = 7850 \text{ kg/m}^3\) \(R \le 0.4 \text{ m}\), \(t \le 0.1 \text{ m}\), \(R, t \ge 0\)

Recalculate Constraints with these parameters:
1. \(g_1(x_1, x_2) = \frac{P}{2\pi x_1 x_2 \sigma_a} - 1 \le 0 \Rightarrow \frac{100 \times 10^3}{2\pi x_1 x_2 (250 \times 10^6)} - 1 \le 0 \Rightarrow \frac{6.366 \times 10^{-5}}{x_1 x_2} - 1 \le 0 \Rightarrow x_1 x_2 \ge 6.366 \times 10^{-5}\)
2. \(g_2(x_1, x_2) = \frac{4 P L^2}{\pi^3 E x_1^3 x_2} - 1 \le 0 \Rightarrow \frac{4 (100 \times 10^3) (5.0)^2}{\pi^3 (210 \times 10^9) x_1^3 x_2} - 1 \le 0 \Rightarrow \frac{1.526 \times 10^{-6}}{x_1^3 x_2} - 1 \le 0 \Rightarrow x_1^3 x_2 \ge 1.526 \times 10^{-6}\)
3. \(g_3(x_1, x_2) = \frac{x_1}{x_2} - 50 \le 0 \Rightarrow x_1 \le 50 x_2 \Rightarrow x_2 \ge \frac{x_1}{50}\) (Assuming \(R/t \le 50\) is for thin-walled tube. If \(R \gg t\), then this constraint ensures it is thin. If we use this as an upper bound on ratio \(R/t\), it’s for manufacturability or avoiding local buckling, as stated in Lecture 2. If it’s \(R/t \ge 10\), that’s for thin-walled assumption. Let’s assume it means \(R \le 50t\).)
Graphical Solution Analysis (Conceptual): The objective is to minimize \(f(x_1, x_2) = 246602.8 x_1 x_2\). The contours are hyperbolas that decrease in value as they approach the origin.
- \(x_1 \ge 0, x_2 \ge 0\) (first quadrant)
- \(x_1 \le 0.4\) (vertical line)
- \(x_2 \le 0.1\) (horizontal line)
- \(g_1: x_1 x_2 \ge 6.366 \times 10^{-5}\) (hyperbola, feasible above)
- \(g_2: x_1^3 x_2 \ge 1.526 \times 10^{-6}\) (steeper curve, feasible above)
- \(g_3: x_2 \ge x_1/50\) (line through origin, feasible above)
The feasible region will be bounded by the outer limits of these constraints and the bounds \(x_1=0.4, x_2=0.1\). To minimize \(x_1 x_2\), we need to find the point in the feasible region closest to the origin. This point will be on one of the “lower” boundaries of the feasible region, meaning where some constraints are active.

Let’s find the intersection points:
- Intersection of \(g_1\) and \(g_2\): From \(g_1\): \(x_2 = \frac{6.366 \times 10^{-5}}{x_1}\) Substitute into \(g_2\): \(x_1^3 \left(\frac{6.366 \times 10^{-5}}{x_1}\right) = 1.526 \times 10^{-6}\) \(6.366 \times 10^{-5} x_1^2 = 1.526 \times 10^{-6}\) \(x_1^2 = \frac{1.526 \times 10^{-6}}{6.366 \times 10^{-5}} \approx 0.02397\) \(x_1 = \sqrt{0.02397} \approx 0.1548 \text{ m}\) Then, \(x_2 = \frac{6.366 \times 10^{-5}}{0.1548} \approx 0.000411 \text{ m}\)
  
  Let’s check if this point \((0.1548, 0.000411)\) is feasible with respect to other constraints:
  - \(x_1 \le 0.4\): \(0.1548 \le 0.4\) (satisfied)
  - \(x_2 \le 0.1\): \(0.000411 \le 0.1\) (satisfied)
  - \(g_3: x_2 \ge x_1/50 \Rightarrow 0.000411 \ge 0.1548/50 \Rightarrow 0.000411 \ge 0.003096\) (NOT satisfied! \(g_3\) is violated). This means the optimum is not at the intersection of \(g_1\) and \(g_2\), but rather on the boundary defined by \(g_3\).
- Intersection of \(g_2\) and \(g_3\): From \(g_3\): \(x_2 = x_1/50\) Substitute into \(g_2\): \(x_1^3 (x_1/50) = 1.526 \times 10^{-6}\) \(x_1^4 / 50 = 1.526 \times 10^{-6}\) \(x_1^4 = 50 \times 1.526 \times 10^{-6} = 7.63 \times 10^{-5}\) \(x_1 = (7.63 \times 10^{-5})^{1/4} \approx 0.0934 \text{ m}\) Then, \(x_2 = x_1/50 = 0.0934/50 = 0.001868 \text{ m}\)
  
  Let’s check if this point \((0.0934, 0.001868)\) is feasible with respect to other constraints:
  - \(x_1 \le 0.4\): \(0.0934 \le 0.4\) (satisfied)
  - \(x_2 \le 0.1\): \(0.001868 \le 0.1\) (satisfied)
  - \(g_1: x_1 x_2 \ge 6.366 \times 10^{-5} \Rightarrow (0.0934)(0.001868) = 0.000174 \ge 6.366 \times 10^{-5}\) (satisfied, inactive)
  Since this point satisfies all constraints, this is a candidate optimum point. At this point, \(x_1^* = 0.0934 \text{ m}\) and \(x_2^* = 0.001868 \text{ m}\). The minimum mass would be \(f(0.0934, 0.001868) = 246602.8 \times 0.0934 \times 0.001868 \approx 42.9 \text{ kg}\).
This graphical approach visually confirms that the optimum solution for two-variable problems often lies at the intersection of active constraints, particularly on the boundary of the feasible region that is “closest” to the direction of optimization for the objective function.

The optimization formulation for Problem 3.22, which involves a cantilever hollow circular beam-column from Exercise 2.23, can be developed by following a five-step procedure: project/problem description, data and information collection, definition of design variables, optimization criterion, and formulation of constraints. The problem aims to translate a descriptive design problem into a well-defined mathematical statement for optimization.

The problem is to solve graphically the cantilever beam problem of Exercise 2.23 [U1]. Exercise 2.23 describes the design of a hollow circular beam-column with outer radius (Ro) and inner radius (Ri). The goal is to minimize mass while satisfying stress and dimension constraints.

{#fig-cantilever-beam)

Specified Data (from Problem 3.22 and Exercise 2.23) [U1, 84]: * Applied load, P = 10 kN = 10,000 N * Length of the beam, L = 5.0 m = 5,000 mm * Modulus of elasticity, E = 210 GPa = 210,000 N/mm² (Note: E is not explicitly used in the stress formulas given for Exercise 2.23, which focuses on bending and shear stresses.) * Allowable bending stress, σa = 250 MPa = 250 N/mm² * Allowable shear stress, τa = 90 MPa = 90 N/mm² * Mass density, ρ = 7850 kg/m³ = 7.85 × 10⁻⁶ kg/mm³ (since 1 m³ = 10⁹ mm³)

1. Definition of Design Variables: The design variables, which are the quantities the designer can change, are the outer and inner radii of the hollow circular cross-section. * Ro (Outer radius, in mm) * Ri (Inner radius, in mm)

2. Optimization Criterion (Objective Function): For structural components, minimizing mass or weight is a common objective. The total mass of the column is given by Mass = ρ * L * A, where A is the cross-sectional area. The cross-sectional area for a hollow circular section is A = π * (Ro² - Ri²).

Therefore, the objective function to be minimized is: Minimize f(Ro, Ri) = ρ * L * π * (Ro² - Ri²) Substituting the given data:

f(Ro, Ri) = (7.85 × 10⁻⁶ kg/mm³) * (5000 mm) * π * (Ro² - Ri²) mm²

f(Ro, Ri) = 0.03925 * π * (Ro² - Ri²) kg

3. Formulation of Constraints: Constraints naturally arise in optimum design problems to ensure the system meets performance requirements and physical limitations. All constraints must be functions of at least one design variable. For numerical optimization, “greater than type” constraints are typically converted to “less than type” (≤ 0) by multiplying by -1.

The constraints for this problem are: * Upper bound on outer radius [U1]: Ro ≤ 20.0 cm = 200 mm g1(Ro, Ri) = Ro - 200 ≤ 0 * Upper bound on inner radius [U1]: Ri ≤ 20.0 cm = 200 mm g2(Ro, Ri) = Ri - 200 ≤ 0 * Inner radius must be less than outer radius: For a hollow section, the inner radius must be strictly smaller than the outer radius (Ri < Ro). g3(Ro, Ri) = Ri - Ro ≤ 0 (Note: For numerical stability, some implementations might use Ri - Ro ≤ -ε where ε is a small positive number, or ensure Ro^4 - Ri^4 is not zero in other ways, as Ro^4 - Ri^4 appears in the denominator of stress calculations). * Non-negativity of radii: Radii must be positive. g4(Ro, Ri) = -Ro ≤ 0 g5(Ro, Ri) = -Ri ≤ 0 * Allowable bending stress: The maximum bending stress (σ) must not exceed the allowable bending stress (σa). σ = (P * L * Ro) / I, where I = (π/4) * (Ro⁴ - Ri⁴) is the moment of inertia. g6(Ro, Ri) = (P * L * Ro) / ((π/4) * (Ro⁴ - Ri⁴)) - σa ≤ 0 Substituting data: g6(Ro, Ri) = (10000 N * 5000 mm * Ro) / ((π/4) * (Ro⁴ - Ri⁴)) - 250 N/mm² ≤ 0 g6(Ro, Ri) = (50,000,000 * Ro) / (0.785398 * (Ro⁴ - Ri⁴)) - 250 ≤ 0 * Allowable shear stress: The maximum shearing stress (τ) must not exceed the allowable shear stress (τa). τ = (P / I) * ((Ro³ + Ri³) / (Ro² + Ri²)). g7(Ro, Ri) = (P * ((Ro³ + Ri³) / (Ro² + Ri²))) / ((π/4) * (Ro⁴ - Ri⁴)) - τa ≤ 0 Substituting data: g7(Ro, Ri) = (10000 N * ((Ro³ + Ri³) / (Ro² + Ri²))) / ((π/4) * (Ro⁴ - Ri⁴)) - 90 N/mm² ≤ 0 g7(Ro, Ri) = (10000 * ((Ro³ + Ri³) / (Ro² + Ri²))) / (0.785398 * (Ro⁴ - Ri⁴)) - 90 ≤ 0

Optimization Formulation: Find the design variables Ro and Ri (in mm).

To Minimize: f(Ro, Ri) = 0.03925 * π * (Ro² - Ri²) (kg)

Subject to the following inequality constraints: 1. g1(Ro, Ri) = Ro - 200 ≤ 0 2. g2(Ro, Ri) = Ri - 200 ≤ 0 3. g3(Ro, Ri) = Ri - Ro ≤ 0 4. g4(Ro, Ri) = -Ro ≤ 0 5. g5(Ro, Ri) = -Ri ≤ 0 6. g6(Ro, Ri) = (50,000,000 * Ro) / (0.785398 * (Ro⁴ - Ri⁴)) - 250 ≤ 0 7. g7(Ro, Ri) = (10000 * ((Ro³ + Ri³) / (Ro² + Ri²))) / (0.785398 * (Ro⁴ - Ri⁴)) - 90 ≤ 0

This problem is a continuous-variable, nonlinear programming (NLP) problem, as the design variables can take any numerical value within their allowed range, and the objective and constraint functions are nonlinear. Due to having only two design variables, it can be solved graphically.

This concludes our exploration of the Graphical Solution Method. It provides a robust foundation for understanding the interaction between objective functions and constraints, and for identifying feasible regions and optimum points. In the next lecture, we will move on to more analytical methods for optimum design, starting with Linear Programming.